• Home
• GitHub
• License (BSD)
• Getting Started
• Install
• Quickstart
• Tutorials
• More Examples
• API Documentation
• API Reference
• Extensions

DiffSharp: Differentiable Tensor Programming Made Simple

DiffSharp is a tensor library with support for differentiable programming. It is designed for use in machine learning, probabilistic programming, optimization and other domains.

Key Features

🗹 Nested and mixed-mode differentiation

🗹 Common optimizers, model elements, differentiable probability distributions

🗹 F# for robust functional programming

🗹 PyTorch familiar naming and idioms, efficient LibTorch CUDA/C++ tensors with GPU support

🗹 Linux, macOS, Windows supported

🗹 Use interactive notebooks in Jupyter and Visual Studio Code

🗹 100% open source

Differentiable Programming

DiffSharp provides world-leading automatic differentiation capabilities for tensor code, including composable gradients, Hessians, Jacobians, directional derivatives, and matrix-free Hessian- and Jacobian-vector products over arbitrary user code. This goes beyond conventional tensor libraries such as PyTorch and TensorFlow, allowing the use of nested forward and reverse differentiation up to any level.

With DiffSharp, you can compute higher-order derivatives efficiently and differentiate functions that are internally making use of differentiation and gradient-based optimization.

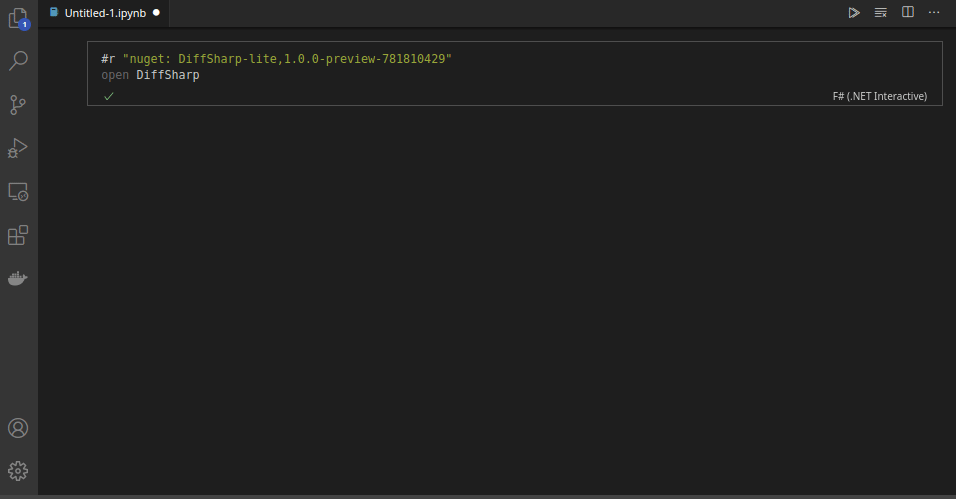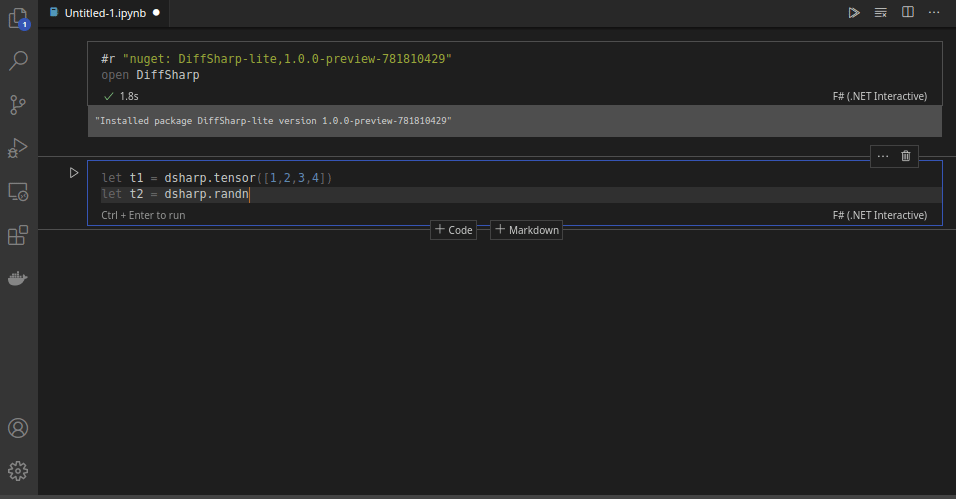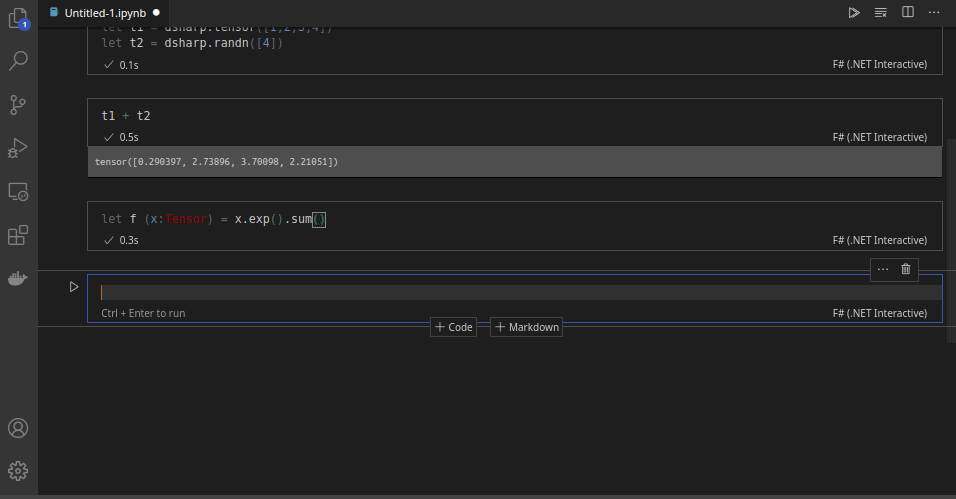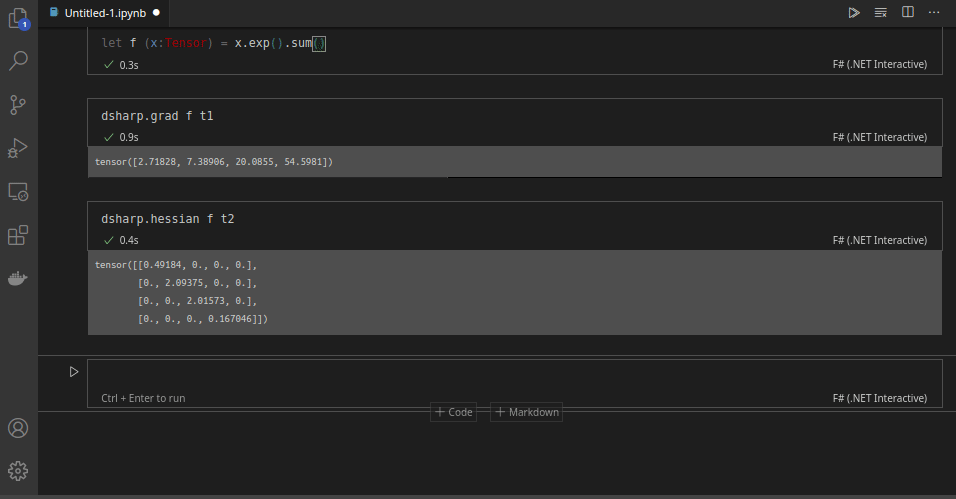
Practical, Familiar and Efficient

DiffSharp comes with a LibTorch backend, using the same C++ and CUDA implementations for tensor computations that power PyTorch. On top of these raw tensors (LibTorch's ATen, excluding autograd), DiffSharp implements its own computation graph and differentiation capabilities. It is tested on Linux, macOS, and Windows, and it supports CUDA and GPUs.

The DiffSharp API is designed to be similar to the PyTorch Python API through very similar naming and idioms, and where elements have similar names the PyTorch documentation can generally be used as a guide.

DiffSharp uses the incredible F# programming language for tensor programming. F# code is generally faster and more robust than equivalent Python code, while still being succinct and compact like Python, making it an ideal modern AI and machine learning implementation language. This allows fluent and productive code for tensor programming.

Interactive Notebooks

All documentation pages in this website are interactive notebooks which you can execute directly in your browser without installing anything in your local machine.

Using the buttons on the top of each page, you can execute the page as an interactive notebook running on cloud servers provided by Google Colab and Binder.

Using the buttons you can also download a page as a script or an interactive notebook, which you can execute locally in Jupyter or Visual Studio Code using dotnet interactive.

Example

Define and add two tensors:

open DiffSharp

let t1 = dsharp.tensor [ 0.0 ..0.2.. 1.0 ] // Gives [0., 0.2, 0.4, 0.6, 0.8, 1.]
let t2 = dsharp.tensor [ 1, 2, 3, 4, 5, 6 ]

t1 + t2

tensor([1.0000, 2.2000, 3.4000, 4.6000, 5.8000, 7.0000])

Compute a convolution:

let t3 = dsharp.tensor [[[[0.0 .. 10.0]]]]
let t4 = dsharp.tensor [[[[0.0 ..0.1.. 1.0]]]]

t3.conv2d(t4)

tensor([[[[38.5000]]]])

Take the gradient of a vector-to-scalar function:

let f (x: Tensor) = x.exp().sum()

dsharp.grad f (dsharp.tensor([1.8, 2.5]))

tensor([ 6.0496, 12.1825])

Compute a nested derivative (checking for perturbation confusion):

let x0 = dsharp.tensor(1)
let y0 = dsharp.tensor(2)
dsharp.diff (fun x -> x * dsharp.diff (fun y -> x * y) y0) x0

No value returned by any evaluator

Define a model and optimize it:

open DiffSharp.Data
open DiffSharp.Model
open DiffSharp.Compose
open DiffSharp.Util
open DiffSharp.Optim

let epochs = 2
let batchSize = 32
let numBatches = 5

let trainSet = MNIST("../data", train=true, transform=id)
let trainLoader = trainSet.loader(batchSize=batchSize, shuffle=true)

let validSet = MNIST("../data", train=false, transform=id)
let validLoader = validSet.loader(batchSize=batchSize, shuffle=false)

let encoder =
    Conv2d(1, 32, 4, 2)
    --> dsharp.relu
    --> Conv2d(32, 64, 4, 2)
    --> dsharp.relu
    --> Conv2d(64, 128, 4, 2)
    --> dsharp.flatten(1)

let decoder =
    dsharp.unflatten(1, [128;1;1])
    --> ConvTranspose2d(128, 64, 4, 2)
    --> dsharp.relu
    --> ConvTranspose2d(64, 32, 4, 3)
    --> dsharp.relu
    --> ConvTranspose2d(32, 1, 4, 2)
    --> dsharp.sigmoid

let model = VAE([1;28;28], 64, encoder, decoder)

let lr = dsharp.tensor(0.001)
let optimizer = Adam(model, lr=lr)

for epoch = 1 to epochs do
    let batches = trainLoader.epoch(numBatches)
    for i, x, _ in batches do
        model.reverseDiff()
        let l = model.loss(x)
        l.reverse()
        optimizer.step()
        print $"Epoch: {epoch} minibatch: {i} loss: {l}" 

let validLoss = 
    validLoader.epoch() 
    |> Seq.sumBy (fun (_, x, _) -> model.loss(x, normalize=false))

print $"Validation loss: {validLoss/validSet.length}"

Numerous other model definition, differentiation, and training patterns are supported. See the tutorials in the left-hand menu and examples on GitHub.

More Information

DiffSharp is developed by Atılım Güneş Baydin, Don Syme and other contributors, having started as a project supervised by the automatic differentiation wizards Barak Pearlmutter and Jeffrey Siskind.

Please join us on GitHub!

© Copyright 2021, DiffSharp Contributors.